Functor

class discopy.monoidal.Functor(ob=None, ar=None, dom=None, cod=None)

Bases: discopy.cat.Functor

A monoidal functor is a functor that preserves the tensor product.

Parameters:

• ob (Mapping[Ty, Ty]) – Map from atomic Ty to cod.ob.

• ar (Mapping[Box, Diagram]) – Map from Box to cod.ar.

• cod (Category) – The codomain of the functor.

• dom (T) –

Important

The keys of the objects mapping must be atomic types, i.e. of length 1.

Example

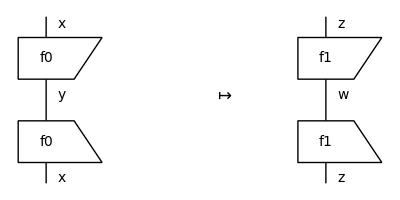
>>> x, y, z, w = Ty('x'), Ty('y'), Ty('z'), Ty('w')
>>> f0, f1 = Box('f0', x, y, data=[0.1]), Box('f1', z, w, data=[1.1])
>>> F = Functor({x: z, y: w, z: x, w: y}, {f0: f1, f1: f0})
>>> assert F(f0) == f1 and F(f1) == f0
>>> assert F(F(f0)) == f0
>>> assert F(f0 @ f1) == f1 @ f0
>>> assert F(f0 >> f0[::-1]) == f1 >> f1[::-1]
>>> source, target = f0 >> f0[::-1], F(f0 >> f0[::-1])

>>> from discopy.drawing import Equation
>>> Equation(source, target, symbol='$\\mapsto$').draw(
...     figsize=(4, 2), path='docs/_static/monoidal/functor-example.png')