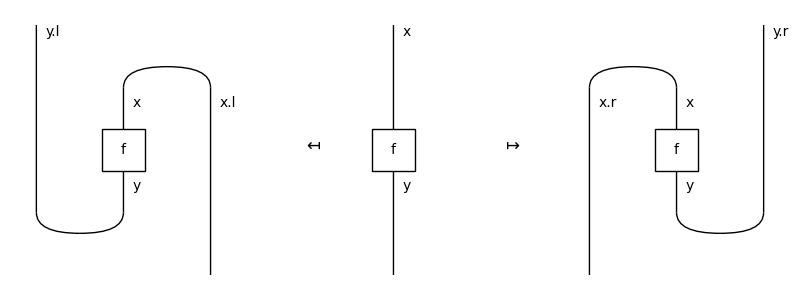
Diagram#
- class discopy.interaction.Diagram(inside, dom, cod)[source]#
Bases:
Composable[Ty],Whiskerable,NamedGeneric['natural']An integer diagram from
xtoyis anaturaldiagram fromx.positive @ y.negativetox.negative @ y.positive.- Parameters:
Note
By default we take
natural = ribbon.Diagrambut this can be any class with the methods for a balanced traced category. For example, the category of boolean matrices with the direct sum has a trace given by reflexive transitive closure. We can use it to check the snake equations:>>> from discopy.matrix import Matrix >>> T, D = Ty[int], Diagram[Matrix[bool]] >>> assert D.id(T(2, 2)).transpose()\ ... == D.id(T(2, 2))\ ... == D.id(T(2, 2)).transpose(left=True)
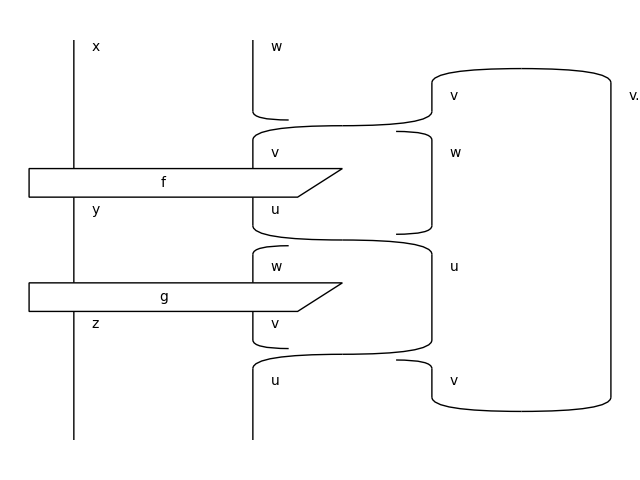
- then(other)[source]#
The composition of two integer diagrams.
- Parameters:
other (Diagram) – The other diagram with which to compose.
Example
>>> from discopy.ribbon import Ty as T, Diagram as D, Box as B >>> u, v, w, x, y, z = map(Ty[T], "uvwxyz") >>> f = Diagram[D](B('f', T('x', 'v'), T('y', 'u')), x @ -u, y @ -v) >>> g = Diagram[D](B('g', T('y', 'w'), T('z', 'v')), y @ -v, z @ -w) >>> (f >> g).draw(path='docs/_static/int/composition.png')
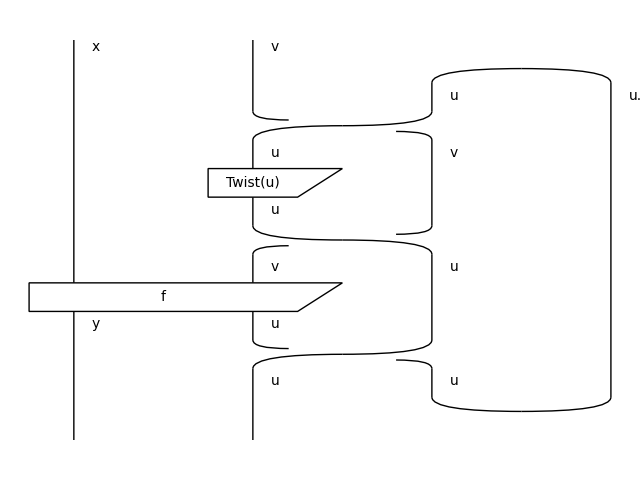
- classmethod id(dom=None)[source]#
The identity on an integer type.
Example
>>> from discopy.ribbon import Ty as T, Diagram as D, Box as B >>> x, y, u, v = map(Ty[T], "xyuv") >>> f = Diagram[D](B('f', T('x', 'v'), T('y', 'u')), x @ -u, y @ -v) >>> (Diagram[D].id(x @ -u) >> f).draw(path='docs/_static/int/idl.png')
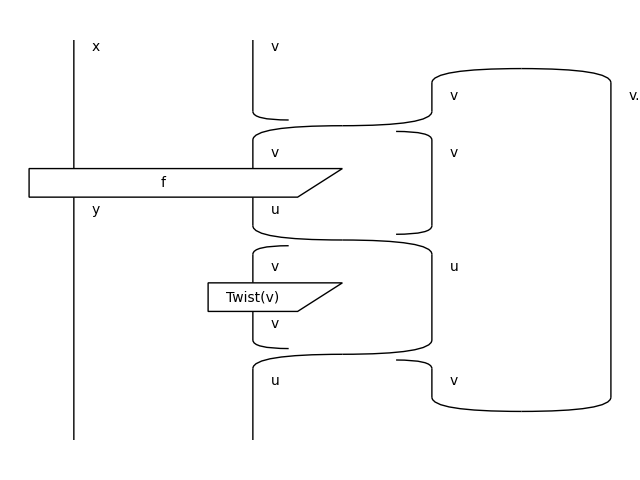
>>> (f >> Diagram[D].id(y @ -v)).draw(path='docs/_static/int/idr.png')
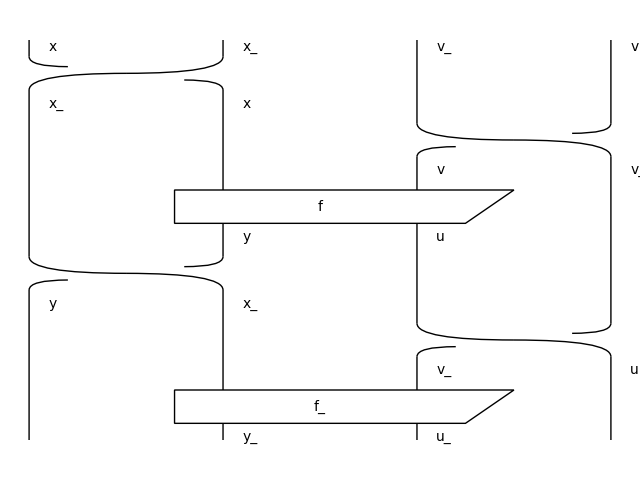
- tensor(other)[source]#
The tensor of two integer diagrams.
- Parameters:
other – The other diagram to tensor.
Example
>>> from discopy.ribbon import Ty as T, Diagram as D, Box as B >>> x, y, u, v = map(Ty[T], "xyuv") >>> x_, y_, u_, v_ = map(lambda x: Ty[T](x + '_'), "xyuv") >>> f = Diagram[D](B('f', T('x', 'v'), T('y', 'u')), x @ -u, y @ -v) >>> f_ = Diagram[D]( ... B('f_', T('x_', 'v_'), T('y_', 'u_')), x_ @ -u_, y_ @ -v_) >>> (f @ f_).draw(path='docs/_static/int/tensor.png')
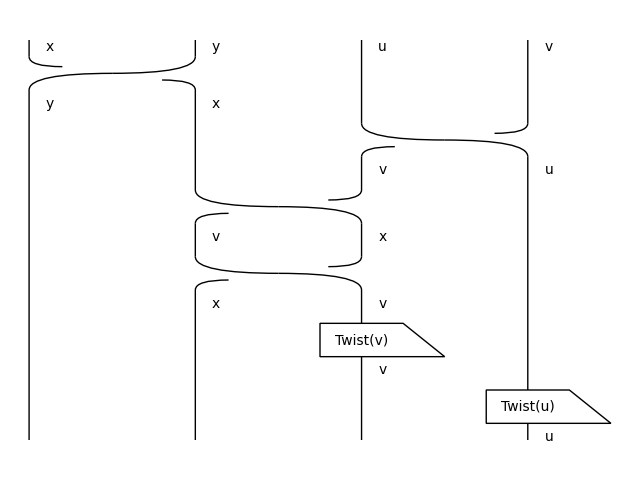
- classmethod braid(left, right)[source]#
The braid of integer diagrams is given by the following diagram:
>>> from discopy.ribbon import Ty as T, Diagram as D, Box as B >>> x, u, y, v = map(Ty[T], "xuyv") >>> Diagram.braid(x @ -u, y @ -v).draw( ... path="docs/_static/int/braid.png")
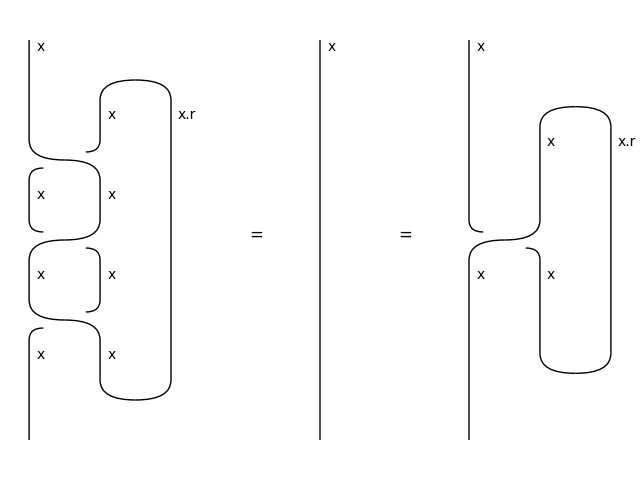
- classmethod cups(left, right)[source]#
The integer cups are given by natural identities.
- Parameters:
- Return type:
Example
This is what the snake equations look like:
>>> from discopy.drawing import Equation >>> x = Ty('x') >>> Equation( ... Diagram.caps(x, -x) @ x >> x @ Diagram.cups(-x, x), ... Diagram.id(x), ... x @ Diagram.caps(-x, x) >> Diagram.cups(x, -x) @ x).draw( ... path="docs/_static/int/int-snake-equations.png")
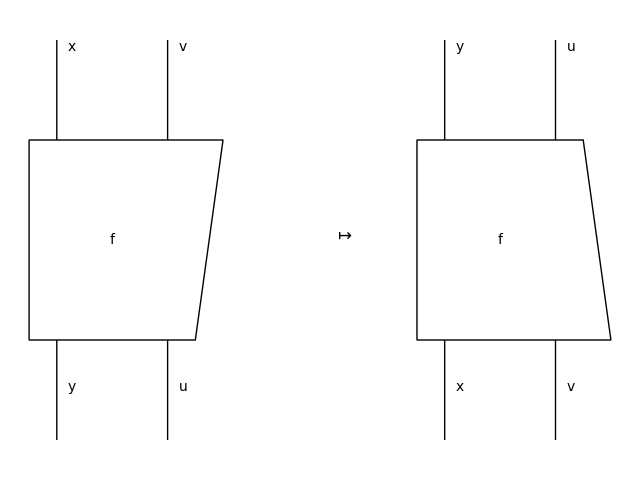
- dagger()[source]#
The dagger of an integer diagram is given by the dagger of its inside.
>>> from discopy.ribbon import Ty as T, Diagram as D, Box as B >>> x, y, u, v = map(Ty[T], "xyuv") >>> f = Diagram[D](B('f', T('x', 'v'), T('y', 'u')), x @ -u, y @ -v) >>> from discopy.drawing import Equation >>> Equation(f, f[::-1], symbol="$\\mapsto$").draw( ... path="docs/_static/int/dagger.png")
- simplify()[source]#
Simplify by going back and forth to
Hypergraph.Example
>>> from discopy import frobenius >>> x = Ty[frobenius.Ty]('x') >>> D = Diagram[frobenius.Diagram] >>> left_snake = D.id(-x).transpose(left=True) >>> right_snake = D.id(-x).transpose(left=False) >>> assert left_snake.simplify() == D.id(x) == right_snake.simplify()
>>> from discopy.drawing import Equation >>> Equation(left_snake, Equation( ... D.id(x), right_snake, symbol="$\\leftarrow$"), ... symbol="$\\rightarrow$").draw( ... path="docs/_static/int/simplify.png")
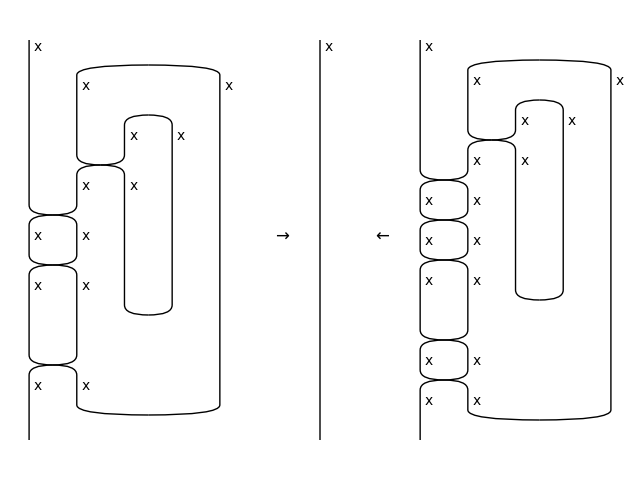
- naturality(i, left=True, down=True, braid=None)[source]#
Slide a box through a braid.
- Parameters:
i (int) – The index of the box to slide.
left – Whether to slide left or right.
down – Whether to slide down or up.
braid – The braiding method to be used.
- Return type:
Examples
>>> x, y, z = map(Ty, "xyz") >>> f = Box('f', x, y) >>> top_left = f @ z >> Braid(y, z) >>> top_right = z @ f >> Braid(z, y) >>> bot_left = Braid(z, x) >> f @ z >>> bot_right = Braid(x, z) >> z @ f >>> assert top_right.naturality(0) == bot_left >>> assert top_left.naturality(0, left=False) == bot_right >>> assert bot_right.naturality(1, down=False) == top_left >>> assert bot_left.naturality(1, left=False, down=False) == top_right
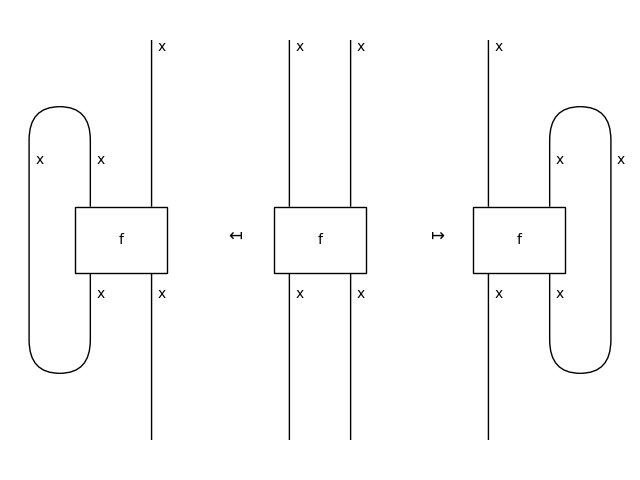
- trace(n=1, left=False)[source]#
Feed
noutputs back into inputs.- Parameters:
n – The number of output wires to feedback into inputs.
left – Whether to trace the wires on the left or right.
Example
>>> from discopy.drawing import Equation as Eq >>> x = Ty('x') >>> f = Box('f', x @ x, x @ x) >>> LHS, RHS = f.trace(left=True), f.trace(left=False) >>> Eq(Eq(LHS, f, symbol="$\\mapsfrom$"), ... RHS, symbol="$\\mapsto$").draw( ... path="docs/_static/traced/trace.png")
- classmethod trace_factory(diagram, left=False)[source]#
The trace of a pivotal diagram is its pre- and post-composition with cups and caps to form a feedback loop.
- Parameters:
diagram (Diagram) – The diagram to trace.
left – Whether to trace on the left or right.
- transpose(left=False)[source]#
The transpose of a diagram, i.e. its composition with cups and caps.
- Parameters:
left – Whether to transpose left or right.
Example
>>> from discopy.drawing import Equation >>> x, y = map(Ty, "xy") >>> f = Box('f', x, y) >>> LHS = Equation(f.transpose(left=True), f, symbol="$\\mapsfrom$") >>> RHS = Equation(LHS, f.transpose(), symbol="$\\mapsto$") >>> RHS.draw(figsize=(8, 3), path="docs/_static/rigid/transpose.png")