closed

The free closed markov category, i.e. with copy, discard and exponentials.

Summary

Ty	A closed type is a biclosed type in a symmetric category where left and right exponentials coincide, i.e. X << Y == X ** Y == Y >> X.
Exp	An exponential object in a markov category.
TermBase	A term in the internal language of a closed category.
Constant
Variable
Application
Abstraction
Diagram	A closed diagram is both a markov and a biclosed diagram.
Box	A closed box is a markov and biclosed box in a closed diagram.
Eval	The evaluation of an exponential type.
Coeval	The coevaluation of an exponential type, i.e. the dagger of an Eval.
Curry	The currying of a closed diagram.
Sum	A markov sum is a symmetric sum and a markov box.
Functor	A closed functor is a markov functor that preserves evaluation and currying.
CMap

Axioms

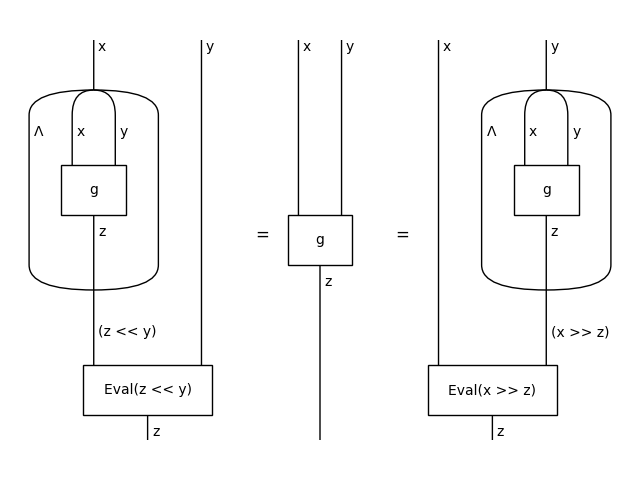
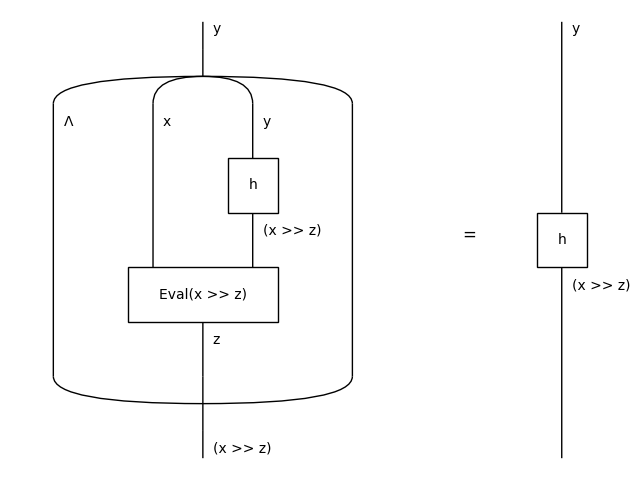
Diagram.curry() and Diagram.uncurry() are inverses.

>>> x, y, z = map(Ty, "xyz")
>>> f, g = Box('f', x, z << y), Box('g', x @ y, z)

>>> from discopy.drawing import Equation
>>> Equation(f.uncurry().curry(), f).draw(
...     path='docs/_static/closed/curry-left.png', margins=(0.1, 0.05))

>>> Equation(g.curry().uncurry(), g).draw(
...     path='docs/_static/closed/uncurry.png')