Diagram

class discopy.symmetric.Diagram(inside, dom, cod, _scan=True)

Bases: discopy.balanced.Diagram

A symmetric diagram is a balanced diagram with Swap boxes.

Parameters:

• inside (Layer) – The layers inside the diagram.

• dom (monoidal.Ty) – The domain of the diagram, i.e. its input.

• cod (monoidal.Ty) – The codomain of the diagram, i.e. its output.

Note

Symmetric diagrams have a class property use_hypergraph_equality, that changes the behaviour of equality and hashing. When set to False, two diagrams equal if they are built from the same layers. When set to True, the underlying hypergraphs are used for hashing and equality checking. The default value of use_hypergraph_equality is False.

>>> x, y = Ty("x"), Ty("y")
>>> id_hash = hash(Id(x @ y))
>>> assert Swap(x, y) >> Swap(y, x) != Id(x @ y)
>>> with Diagram.hypergraph_equality:
...     assert Swap(x, y) >> Swap(y, x) == Id(x @ y)
...     assert id_hash != hash(Id(x @ y))

Note

Symmetric diagrams can be defined using the standard syntax for functions.

>>> x = Ty('x')
>>> f = Box('f', x @ x, x)
>>> g = Box('g', x, x @ x)

>>> @Diagram.from_callable(x @ x @ x, x @ x @ x)
... def diagram(x0, x1, x2):
...     x3 = f(x2, x0)
...     x4, x5 = g(x1)
...     return x5, x3, x4
>>> diagram.draw(draw_type_labels=False,
...              path='docs/_static/symmetric/decorator.png')

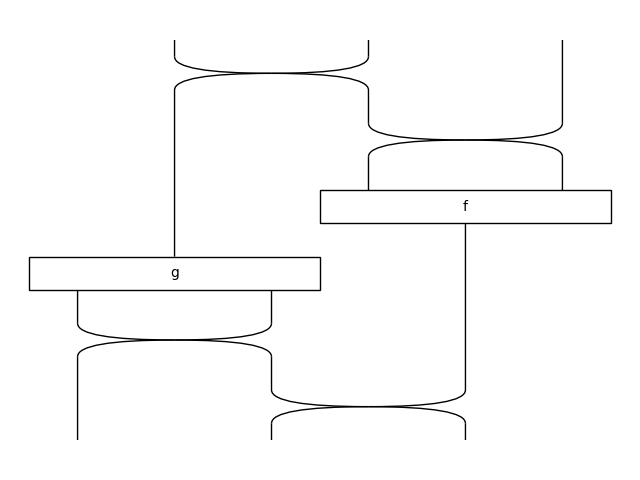
Every variable must be used exactly once or this will raise an error.

>>> from pytest import raises
>>> from discopy.utils import AxiomError

>>> with raises(AxiomError) as err:
...     Diagram.from_callable(x, x @ x)(lambda x: (x, x))
>>> print(err.value)
symmetric.Diagram does not have copy or discard.

>>> with raises(AxiomError) as err:
...     Diagram.from_callable(x, Ty())(lambda x: ())
>>> print(err.value)
symmetric.Diagram does not have copy or discard.

Note

As for discopy.balanced.Diagram, our symmetric diagrams are traced by default. However now we have that the axioms for trace hold on the nose.

classmethod swap(left, right)

The diagram that swaps the left and right wires.

Parameters:

• left (Ty) – The type at the top left and bottom right.

• right (Ty) – The type at the top right and bottom left.

Return type:

Diagram

Note

This calls balanced.hexagon() and braid_factory.

classmethod permutation(xs, dom=None)

The diagram that encodes a given permutation.

Parameters:

• xs (list[int]) – A list of integers representing a permutation.

• dom (Ty | None) – A type of the same length as permutation, default is PRO(len(permutation)).

Return type:

Diagram

permute(*xs)

Post-compose with a permutation.

Parameters:

xs (int) – A list of integers representing a permutation.

Return type:

Diagram

Examples

>>> x, y, z = Ty('x'), Ty('y'), Ty('z')
>>> assert Id(x @ y @ z).permute(2, 0, 1).cod == z @ x @ y

to_hypergraph()

Translate a diagram into a hypergraph.

Return type:

Hypergraph

simplify()

Simplify by translating back and forth to hypergraph.

depth()

The depth of a symmetric diagram.

Examples

>>> x = Ty('x')
>>> f = Box('f', x, x)
>>> assert Id(x).depth() == Id().depth() == 0
>>> assert f.depth() == (f @ f).depth() == 1
>>> assert (f @ f >> Swap(x, x)).depth() == 1
>>> assert (f >> f).depth() == 2 and (f >> f >> f).depth() == 3

braid_factory

alias of Swap

factory

alias of Diagram

sum_factory

alias of Sum

trace_factory

alias of Trace