Functor

Contents

Functor#

class discopy.tensor.Functor(ob, ar, dom=None, dtype=<class 'int'>)[source]#

Bases: Functor

A tensor functor is a frobenius functor with a domain category dom and Category(Dim, Tensor[dtype]) as codomain for a given dtype.

Parameters:

  • ob (dict[cat.Ob, Dim]) – The object mapping.

  • ar (dict[cat.Box, list]) – The arrow mapping.

  • dom (T) – The domain of the functor.

  • dtype (type) – The datatype for the codomain Category(Dim, Tensor[dtype]).

Example

>>> n, s = map(rigid.Ty, "ns")
>>> Alice = rigid.Box('Alice', rigid.Ty(), n)
>>> loves = rigid.Box('loves', rigid.Ty(), n.r @ s @ n.l)
>>> Bob = rigid.Box('Bob', rigid.Ty(), n)
>>> diagram = Alice @ loves @ Bob\
...     >> rigid.Cup(n, n.r) @ s @ rigid.Cup(n.l, n)

>>> F = Functor(
...     ob={s: 1, n: 2},
...     ar={Alice: [0, 1], loves: [0, 1, 1, 0], Bob: [1, 0]},
...     dom=rigid.Category(), dtype=bool)
>>> F(diagram)
Tensor[bool]([True], dom=Dim(1), cod=Dim(1))

>>> rewrite = diagram\
...     .transpose_box(2).transpose_box(0, left=True).normal_form()
>>> from discopy.drawing import Equation
>>> Equation(diagram, rewrite).draw(
...     figsize=(8, 3), path='docs/_static/tensor/rewrite.png')
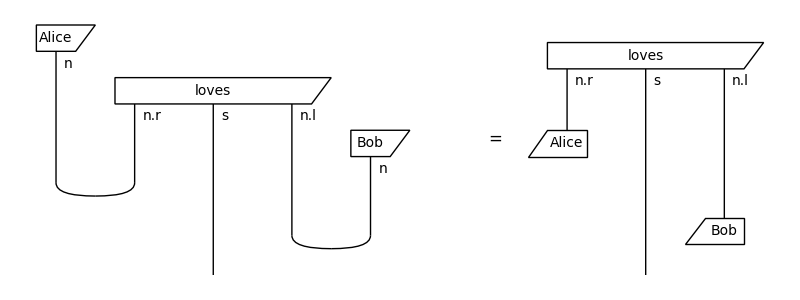
../_images/rewrite.png 
>>> assert F(diagram) == F(rewrite)
Contents