Diagrammatic Differentiation

Quantum Group Workshop, 26th January 2021

Alexis Toumi, joint work with Richie Yeung and Giovanni de Felice

https://doi.org/10.4204/EPTCS.343.7

1) Parametrised matrices

Fix a rig \((\mathbb{S}, +, \times, 0, 1)\).

Definition: A matrix \(f \in \mathbf{Mat}_\mathbb{S}(m, n)\) is a function \(f : [m] \times [n] \to \mathbb{S}\) where \([n] = \{0, \dots, n - 1\}\) for \(n \in \mathbb{N}\).

Definition: A parametrised matrix is a function \(f : \mathbb{S} \to \mathbf{Mat}_\mathbb{S}(m, n)\), or equivalently a function-valued matrix \(f \in \mathbf{Mat}_{\mathbb{S} \to \mathbb{S}}(m, n)\).

Example:

from discopy.quantum.gates import Rz
from sympy import Expr
from sympy.abc import phi

Rz(phi).array

array([[exp(-1.0*I*pi*phi), 0],
       [0, exp(1.0*I*pi*phi)]], dtype=object)

(lambda phi: Rz(phi).array)(0.25)

array([[0.70710678-0.70710678j, 0.        +0.j        ],
       [0.        +0.j        , 0.70710678+0.70710678j]])

2) Parametrised diagrams

Fix a monoidal signature \((\Sigma_0, \Sigma_1, \text{dom}, \text{cod} : \Sigma_1 \to \Sigma_0^\star)\) for \(X^\star = \coprod_{n \in \mathbb{N}} X^n\) the free monoid.

Definition: An abstract diagram \(d \in \mathbf{C}_\Sigma(s, t)\) is defined by a list of \(\text{layers}(d) = (\text{left}_0, \text{box}_0, \text{right}_0), \dots, (\text{left}_n, \text{box}_n, \text{right}_n) \in \Sigma_0^\star \times \Sigma_1 \times \Sigma_0^\star\).

Definition: A concrete diagram is an abstract diagram with a monoidal functor \(F : \mathbf{C}_\Sigma \to \mathbf{Mat}_\mathbb{S}\).

Definition: A parametrised diagram is a function \(d : \mathbb{S} \to \mathbf{C}_\Sigma(s, t)\), or equivalently, a diagram with a monoidal functor \(F : \mathbf{C}_\Sigma \to \mathbf{Mat}_{\mathbb{S} \to \mathbb{S}}\).

Example:

from discopy.tensor import Dim, Box

x, y, z = Dim(1), Dim(2), Dim(2)
f = Box('f', x, y, [phi + 1, -phi * 2])
g = Box('g', y @ y, z, [1, 0, 0, 0, 0, 0, 0, phi ** 2 + 1])

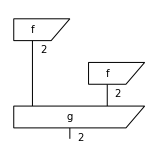
d = f @ f >> g
print(d)
d.draw(figsize=(2, 2))

d.eval(dtype=Expr).array

f >> Dim(2) @ f >> g

array([(phi + 1)**2, 4*phi**2*(phi**2 + 1)], dtype=object)

d.subs(phi, 0.25).eval(dtype=Expr).array

array([1.5625, 0.265625], dtype=object)

3) Product rule

We define the gradient of a parametrised matrix \(f \in \mathbf{Mat}_{\mathbb{S} \to \mathbb{S}}(m, n)\) elementwise:

\[\frac{\partial f}{\partial x}(i, j) = \frac{\partial}{\partial x} f(i, j)\]

Given a parametrised diagram \(d, F\) we want a new diagram \(\frac{\partial d}{\partial x}\) such that:

\[F\big(\frac{\partial d}{\partial x}\big) = \frac{\partial F(d)}{\partial x}\]

We can do this by defining gradients as formal sums of diagrams and using the product rule:

\[\frac{\partial}{\partial x} (d \otimes d') = \frac{\partial d}{\partial x} \otimes d' + d \otimes \frac{\partial d'}{\partial x}\]

\[\frac{\partial}{\partial x} (d \circ d') = \frac{\partial d}{\partial x} \circ d' + d \circ \frac{\partial d'}{\partial x}\]

Example:

d.grad(phi).draw(figsize=(8, 3), draw_type_labels=False)

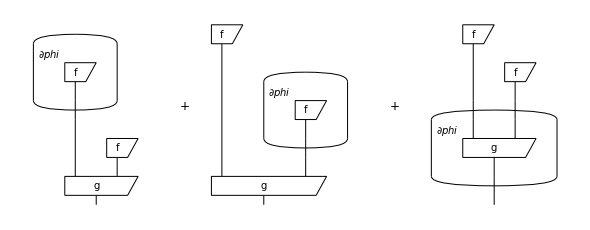
4) Chain rule

Given an arbitrary function \(f : \mathbb{S} \to \mathbb{S}\), we lift it to matrices by applying it elementwise. Diagrammatically, we represent this as a bubble around a subdiagram.

Gradients of bubbles are then given by the chain rule:

\[\frac{\partial}{\partial x} f(d) = \frac{\partial f}{\partial x} (d) \times \frac{\partial d}{\partial x}\]

where the elementwise product can be encoded as pre- and post-composition with spiders.

g = Box('g', Dim(2), Dim(2), [2 * phi, 0, 0, phi + 1])
f = lambda d: d.bubble(func=lambda x: x ** 2, drawing_name="f")
lhs, rhs = Box.grad(f(g), phi), f(g).grad(phi)

from discopy.drawing import Equation
Equation(lhs, rhs).draw(draw_type_labels=False)

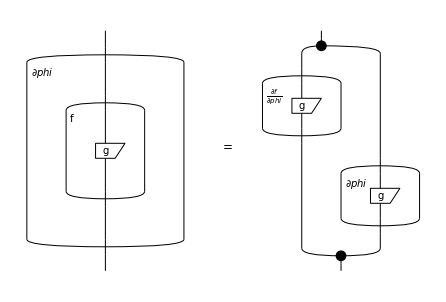
5) Applications

• Gradients of quantum circuits using the parameter shift rule.

• Gradients of neural nets and classical post-processing with bubbles.

• Gradients of circuit functors for QNLP.