compact

The free compact category, i.e. diagrams with swaps, cups and caps.

Summary

Diagram	A compact diagram is a symmetric diagram and a ribbon diagram.
Box	A compact box is a symmetric and ribbon box in a compact diagram.
Cup	A compact cup is a ribbon cup in a compact diagram.
Cap	A compact cap is a ribbon cap in a compact diagram.
Swap	A compact swap is a symmetric swap and a ribbon braid.
Category	A compact category is both a symmetric category and a ribbon category.
Functor	A compact functor is both a symmetric functor and a ribbon functor.

Axioms

>>> from discopy.drawing import Equation
>>> Diagram.use_hypergraph_equality = True
>>> x, y = Ty('x'), Ty('y')

Snake equations

>>> snake = Equation(Id(x.l).transpose(left=True), Id(x), Id(x.r).transpose())
>>> assert snake
>>> snake.draw(path="docs/_static/compact/snake.png")

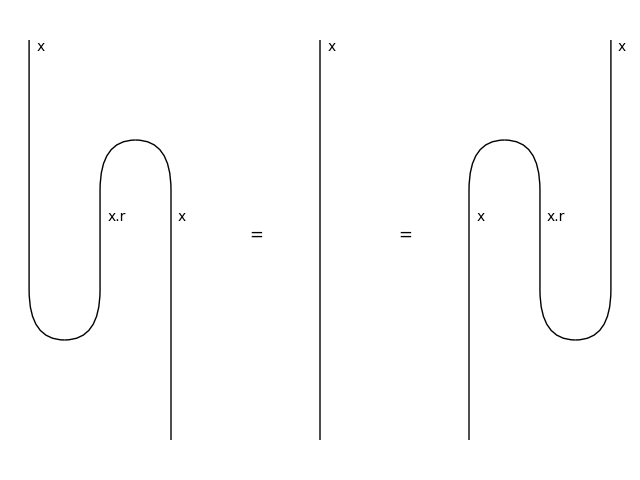
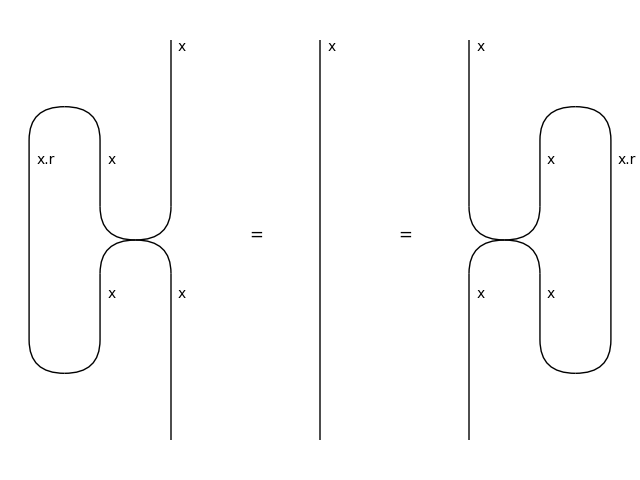
Yanking

a.k.a. Reidemeister move 1

>>> right_loop = x @ Cap(x, x.r) >> Swap(x, x) @ x.r >> x @ Cup(x, x.r)
>>> left_loop = Cap(x.r, x) @ x >> x.r @ Swap(x, x) >> Cup(x.r, x) @ x
>>> yanking = Equation(left_loop, Id(x), right_loop)
>>> assert yanking
>>> yanking.draw(path="docs/_static/compact/yanking.png")

>>> cap_yanking = Equation(Cap(x, x.r) >> Swap(x, x.r), Cap(x.r, x))
>>> cup_yanking = Equation(Swap(x, x.r) >> Cup(x.r, x), Cup(x, x.r))
>>> assert cap_yanking and cup_yanking
>>> Equation(cap_yanking, cup_yanking, symbol='', space=1).draw(
...     figsize=(6, 3), path="docs/_static/compact/yanking_cup_and_cap.png")

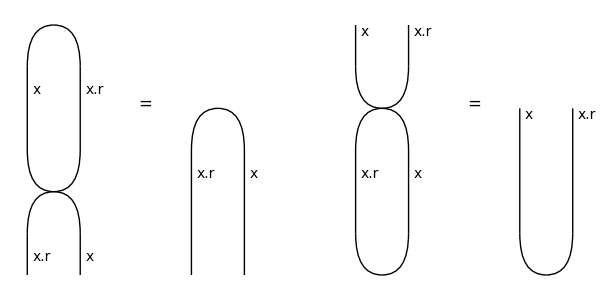
Coherence

>>> assert Diagram.caps(x @ y, y.r @ x.r)\
...     == Cap(x, x.r) @ Cap(y, y.r) >> x @ Diagram.swap(x.r, y @ y.r)

>>> Diagram.use_hypergraph_equality = False