stream

The feedback category of monoidal streams over a symmetric monoidal category.

We adapted the definition of intensional streams from Di Lavore et al. [DLdeFeliceRoman22].

Summary

Ty	A stream of types from some underlying class base.
Stream	Monoidal streams over an underlying category.
Category	Syntactic sugar for Category(Ty[category.ob], Stream[category]).

Note

Monoidal streams form a feedback category as follows:

>>> from discopy import feedback, drawing
>>> x, y, m = map(feedback.Ty, "xym")
>>> f = feedback.Box('f', x @ m.delay(), y @ m)
>>> fb = f.feedback()

>>> X, Y, M = [Ty.sequence(symmetric.Ty(n)) for n in "xym"]
>>> Ff = Stream.sequence("f", X @ M.delay(), Y @ M)

>>> F = feedback.Functor(ob={x: X, y: Y, m: M}, ar={f: Ff},
...                      cod=feedback.Category(Ty, Stream))

>>> drawing.Equation(fb, F(fb).unroll(2).now, symbol="$\\mapsto$").draw(
...     path="docs/_static/stream/feedback-to-stream.png")

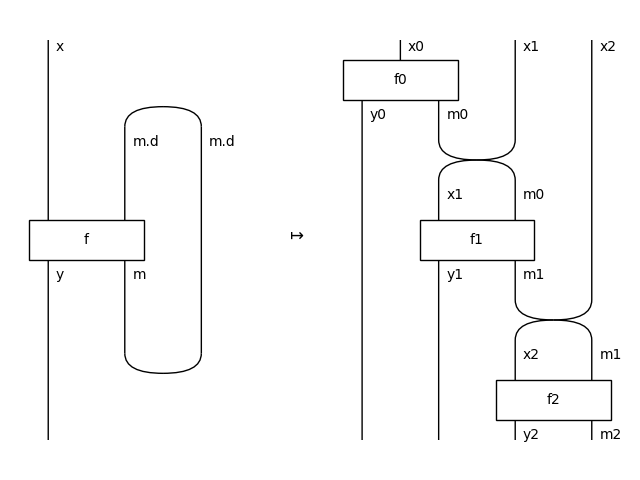
Examples

We can define the Fibonacci sequence as a feedback diagram interpreted in the category of streams of python types and functions.

>>> from discopy import *
>>> from discopy.feedback import *

>>> X = Ty('X')
>>> fby, wait = FollowedBy(X), Swap(X, X.d).feedback()
>>> zero, one = Box('zero', Ty(), X.head), Box('one', Ty(), X.head)
>>> copy, plus = Copy(X), Box('plus', X @ X, X)

>>> @Diagram.feedback
... @Diagram.from_callable(X.d, X @ X)
... def fib(x):
...     y = fby(zero(), plus.d(fby.d(one.d(), wait.d(x)), x))
...     return (y, y)

>>> fib_ = (copy.d >> one.d @ wait.d @ X.d
...                >> fby.d @ X.d
...                >> plus.d
...                >> zero @ X.d
...                >> fby >> copy).feedback()
>>> with Diagram.hypergraph_equality:
...     assert fib == fib_
>>> fib_.draw(draw_type_labels=False, figsize=(5, 5),
...           path="docs/_static/stream/fibonacci-feedback.png")

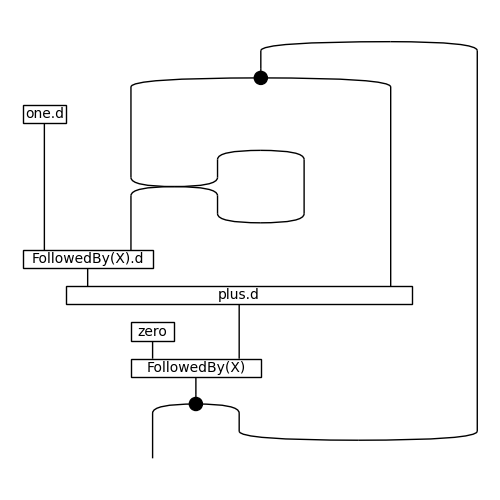
>>> cod = stream.Category(python.Ty, python.Function)
>>> F = feedback.Functor(
...     ob={X: int},
...     ar={zero: cod.ar.singleton(python.Function(lambda: 0, (), int)),
...         one: cod.ar.singleton(python.Function(lambda: 1, (), int)),
...         plus: lambda x, y: x + y}, cod=cod)
>>> assert F(fib).unroll(9).now()[:10] == (0, 1, 1, 2, 3, 5, 8, 13, 21, 34)

We can define a simple random walk as a feedback diagram interpreted in the category of streams of python types and probabilistic functions.

>>> from random import choice, seed; seed(420)
>>> rand = Box('rand', Ty(), X)
>>> F.ar[rand] = lambda: choice([-1, +1])

>>> @Diagram.feedback
... @Diagram.from_callable(X.d, X @ X)
... def walk(x):
...     x = plus.d(rand.d(), x)
...     x = fby(zero(), x)
...     return (x, x)

>>> walk.draw(draw_type_labels=False, figsize=(5, 5),
...           path="docs/_static/stream/random-walk-feedback.png")

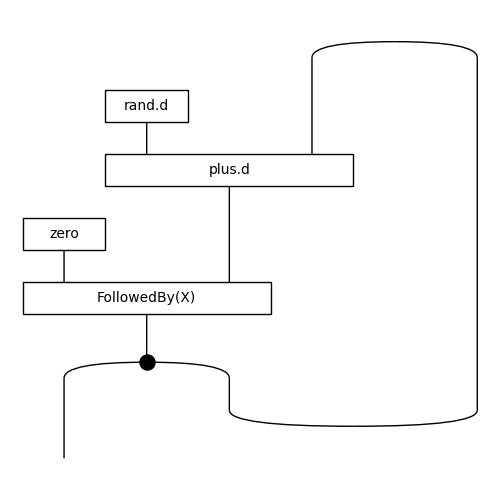
>>> assert F(walk).unroll(9).now()[:10] == (0, -1, 0, 1, 2, 1, 0, -1, 0, 1)
>>> assert F(walk).unroll(9).now()[:10] == (0, -1, -2, -1, 0, 1, 0, 1, 2, 1)
>>> assert F(walk).unroll(9).now()[:10] == (0, -1, 0, 1, 0, 1, 0, -1, 0, -1)

Note that we can only check equality of streams up to a finite number of steps.

>>> from discopy.stream import *
>>> all_eq = lambda xs: len(set(xs)) == 1
>>> eq_up_to_n = lambda *xs, n=3: all_eq(x.unroll(n).now for x in xs)

>>> x, y, z, w, m, n, o = map(Ty.sequence, "xyzwmno")
>>> f = Stream.sequence('f', x, y, m)
>>> g = Stream.sequence('g', y, z, n)
>>> h = Stream.sequence('h', z, w, o)

• Unitality and associativity hold on the nose:

>>> _id = Stream.id
>>> assert eq_up_to_n(f @ _id(), f, _id() @ f)
>>> assert eq_up_to_n(f >> _id(f.cod), f, _id(f.dom) >> f)
>>> assert eq_up_to_n((f >> g) >> h), (f >> (g >> h))
>>> ((f >> g) >> h).now.draw(
...     path="docs/_static/stream/feedback-associativity.png")

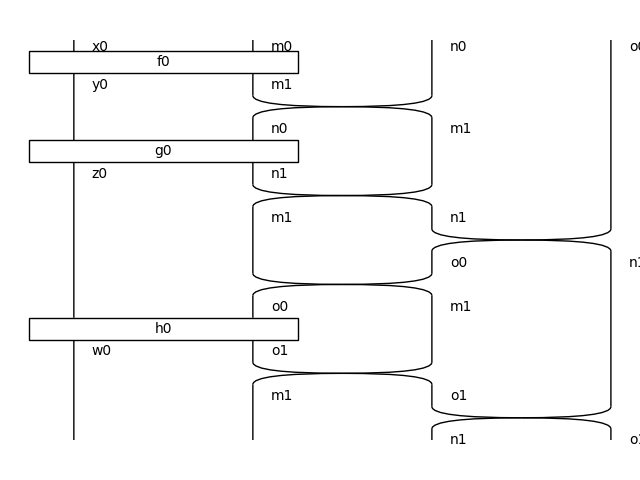
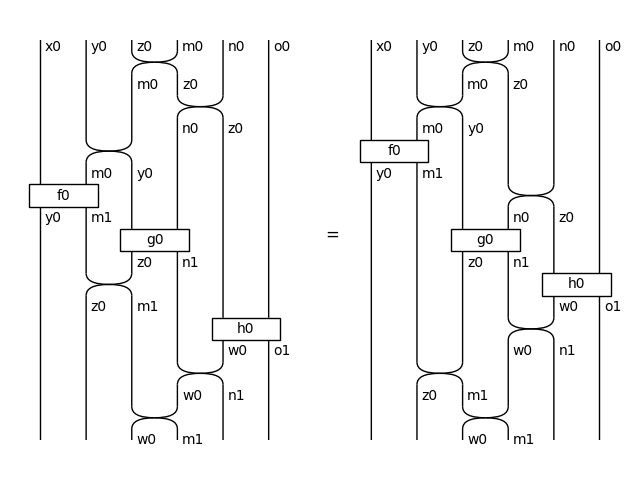
• Associativity of tensor holds up to interchanger:

>>> from discopy.drawing import Equation
>>> drawing.Equation(*map(lambda x: x.now, ((f @ g) @ h, f @ (g @ h)))).draw(
...     path="docs/_static/stream/feedback-tensor-associativity.png")

>>> eq_up_to_interchanger = lambda *xs: all_eq(
...     monoidal.Diagram.normal_form(x.now) for x in xs)
>>> assert eq_up_to_interchanger((f @ g) @ h, f @ (g @ h))

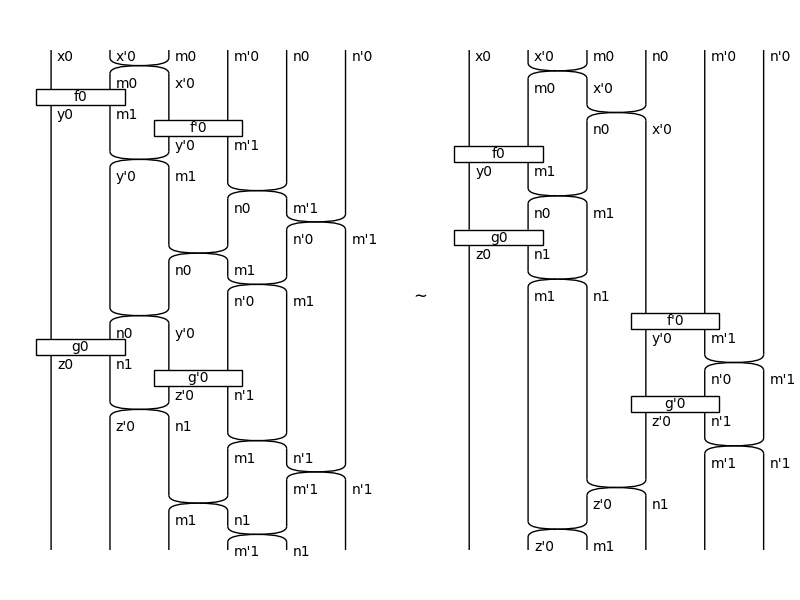
• Interchanger holds up to permutation of the memories:

>>> x_, y_, z_, m_, n_ = [
...     Ty.sequence(symmetric.Ty(name + "'")) for name in "xyzmn"]
>>> f_ = Stream.sequence("f'", x_, y_, m_)
>>> g_ = Stream.sequence("g'", y_, z_, n_)

>>> LHS, RHS = f @ f_ >> g @ g_, (f >> g) @ (f_ >> g_)
>>> drawing.Equation(LHS.now, RHS.now, symbol="$\\sim$").draw(
...     path="docs/_static/stream/feedback-interchanger.png", figsize=(8, 6))

>>> pi, id_dom = (0, 1, 2, 4, 3, 5), symmetric.Id(LHS.now.dom)
>>> with symmetric.Diagram.hypergraph_equality:
...     assert LHS.now == id_dom.permute(*pi) >> RHS.now.permute(*pi)

See discopy.feedback for the other axioms for feedback categories.