Diagram#
- class discopy.grammar.pregroup.Diagram(inside, dom, cod, _scan=True)[source]#
Bases:
DiagramA pregroup diagram is a rigid diagram with
Wordboxes.- Parameters:
Note
In order to define more general DisCoCat diagrams, pregroup diagrams subclass frobenius rather than rigid. Have fun with swaps and spiders!
Example
>>> s, n = Ty('s'), Ty('n') >>> Alice, Bob = Word('Alice', n), Word('Bob', n) >>> loves = Word('loves', n.r @ s @ n.l) >>> grammar = Cup(n, n.r) @ Id(s) @ Cup(n.l, n) >>> sentence = grammar << Alice @ loves @ Bob >>> print(sentence[:4]) Alice >> n @ loves >> n @ n.r @ s @ n.l @ Bob >> Cup(n, n.r) @ s @ n.l @ n >>> from discopy import tensor >>> ob = {s: 1, n: 2} >>> ar = {Alice: [1, 0], loves: [0, 1, 1, 0], Bob: [0, 1]} >>> F = tensor.Functor(ob, ar, dom=Category(), dtype=bool) >>> assert F(sentence)
- ty_factory#
alias of
Ty
- normal_form(**params)[source]#
Applies normal form to a pregroup diagram of the form
word @ ... @ word >> wiresby normalising words and wires seperately before combining them, so it can be drawn withdraw().
- classmethod cups(left, right)[source]#
Construct a diagram of nested cups for types
leftandright.- Parameters:
- Return type:
Example
>>> a, b = Ty('a'), Ty('b') >>> Diagram.cups(a.l @ b, b.r @ a).draw(figsize=(3, 1),\ ... margins=(0.3, 0.05), path='docs/_static/rigid/cups.png')
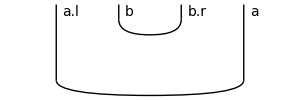
- classmethod caps(left, right)[source]#
Construct a diagram of nested caps for types
leftandright.- Parameters:
- Return type:
Example
>>> a, b = Ty('a'), Ty('b') >>> Diagram.caps(a.r @ b, b.l @ a).draw(figsize=(3, 1),\ ... margins=(0.3, 0.05), path='docs/_static/rigid/caps.png')
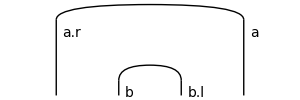
- spider_factory#
alias of
Spider