feedback

The free feedback category, i.e. diagrams with delayed feedback loops.

We follow the definition of Di Lavore et al. [DLdeFeliceRoman22] with some extra structure for the head and tail of streams with the FollowedBy generator.

The main example of a feedback category is given by discopy.stream.

Summary

Ob	A feedback object is an object with a time_step and an optional argument is_constant for whether the object is interpreted as a constant stream.
HeadOb	The head of a feedback object, interpreted as the first element of a stream followed by the constant stream on the empty type.
TailOb	The tail of a non-constant feedback object, interpreted as the stream starting from the second time step.
Ty	A feedback type is a monoidal type with delay, head and tail.
Layer	A feedback layer is a monoidal layer with a delay method.
Diagram	A feedback diagram is a markov diagram with a delay() endofunctor and a feedback() operator.
Box	A feedback box is a markov box in a feedback diagram.
Swap	The swap of feedback types left and right.
Feedback	Feedback is a bubble that takes a diagram from dom @ mem.delay() to cod @ mem and returns a box from dom to cod.
FollowedBy	The isomorphism between x.head @ x.tail.delay() and x.
Head	The head of a feedback diagram, interpreted as the first element followed by the identity stream on the empty type.
Tail	The tail of a feedback diagram, interpreted as the stream starting from the second time step with the identity on the empty type at the first step.
Category	A feedback category is a markov category with methods delay and feedback.
Functor	A feedback functor is a markov one that preserves delay and feedback.

Axioms

A feedback category is a symmetric monoidal category with a monoidal endofunctor Diagram.delay(), shortened to .d and a method Diagram.feedback() of the following shape:

>>> from discopy.drawing import Equation

>>> x, y, m = map(Ty, "xym")
>>> f = Box('f', x @ m.delay(), y @ m)
>>> Equation(f, f.feedback(), symbol="$\\mapsto$").draw(
...     path="docs/_static/feedback/feedback-operator.png", figsize=(8, 4))

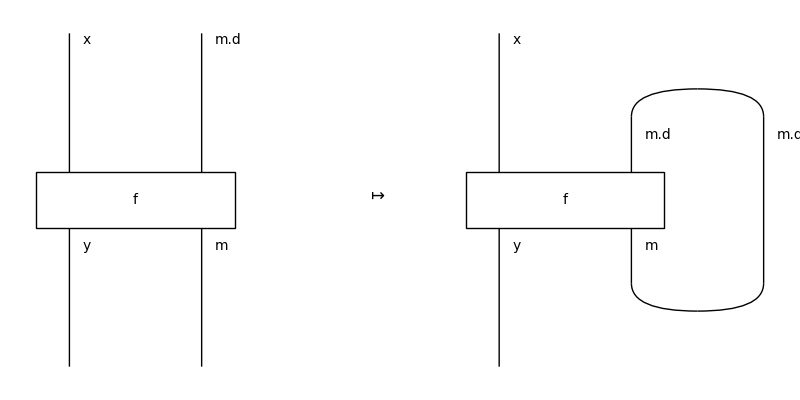
such that the following equations are satisfied:

Vanishing

>>> assert Box('f', x, y).feedback(mem=Ty()) == Box('f', x, y)

Joining

>>> f = Box('f', x @ (m @ m).delay(), y @ m @ m)
>>> assert f.feedback(mem=m @ m) == f.feedback().feedback()

Strength

This can only be checked up to a functor into streams.

>>> from discopy import stream
>>> F0 = Functor(lambda x: stream.Ty.sequence(x.name), cod=stream.Category())
>>> F = Functor(
...     F0, lambda f: stream.Stream.sequence(f.name, F0(f.dom), F0(f.cod)),
...     cod=stream.Category())
>>> all_eq = lambda xs: len(set(xs)) == 1
>>> eq_up_to_F = lambda *fs, n=2: all_eq(F(f).unroll(2).now for f in fs)

>>> f, g = Box('f', x @ m.delay(), y @ m), Box('g', x, y)
>>> strength = Equation(g @ f.feedback(), (g @ f).feedback())
>>> assert eq_up_to_F(*strength.terms)
>>> strength.draw(
...     path='docs/_static/feedback/strength.png', draw_type_labels=False)

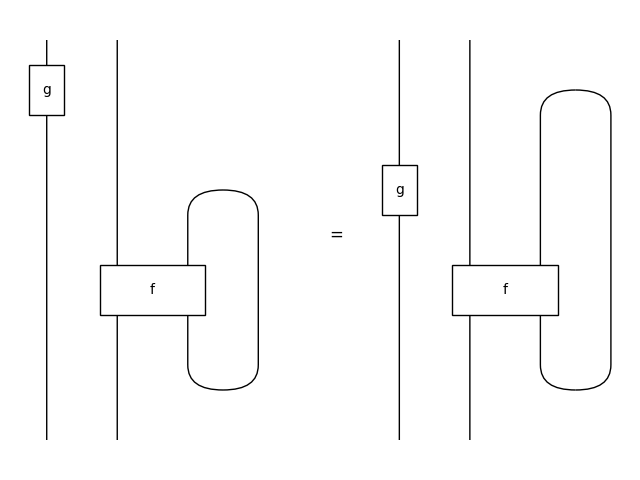
Sliding

This can only be checked up to extensional equivalence of streams.

>>> from discopy import symmetric
>>> n = Ty("n")
>>> h = Box('h', m, n)  # assume h is an isomorphism
>>> f = Box('f', x @ n.d, y @ m)
>>> sliding = Equation((f >> y @ h).feedback(), (x @ h.d >> f).feedback())
>>> sliding.draw(
...     path='docs/_static/feedback/sliding.png', draw_type_labels=False)

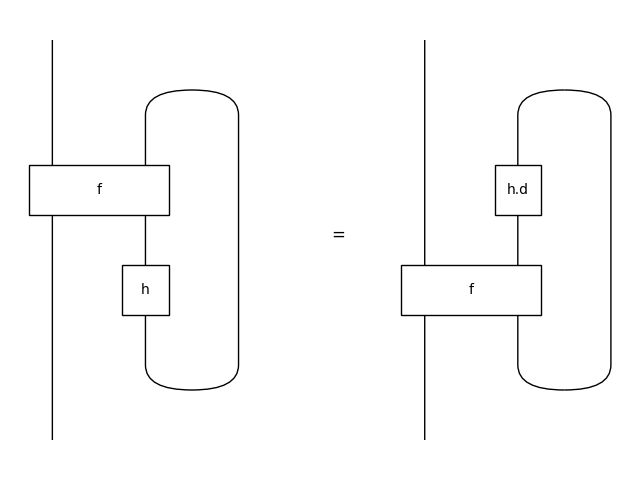
>>> LHS, RHS = sliding.terms
>>> eq = Equation(*map(lambda f: F(f).unroll(2).now, sliding.terms),
...     symbol="$\\sim$").draw(path='docs/_static/feedback/slide-unroll.png')
>>> with symmetric.Diagram.hypergraph_equality:
...     assert F(LHS).unroll(2).now == F(RHS).unroll(2).now\
...         >> F(y).unroll(2).now @ F(h).later.later.now

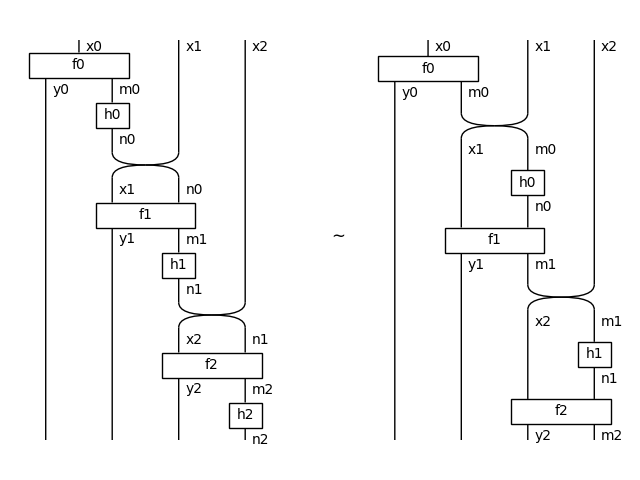
Note

Every traced symmetric category is a feedback category with a trivial delay:

>>> from discopy import symmetric
>>> symmetric.Ty.delay = symmetric.Diagram.delay = lambda self: self
>>> symmetric.Diagram.feedback = lambda self, dom=None, cod=None, mem=None:\
...     self.trace(len(mem))

>>> F0 = Functor(
...     ob=lambda x: symmetric.Ty(x.name), ar={}, cod=symmetric.Category)
>>> assert F0(x.delay()) == F0(x)

>>> F = Functor(
...     ob=F0, ar=lambda f: symmetric.Box(f.name, F0(f.dom), F0(f.cod)),
...     cod=symmetric.Category)
>>> f = Box('f', x @ m.delay(), y @ m)
>>> assert F(f.delay()) == F(f) and F(f.feedback()) == F(f).trace()

Note

We also implement endofunctors Head and Tail together with an isomorphism FollowedBy between x and x.head @ x.tail.delay().

This satisfies the following equations:

>>> assert x.head.head == x.head
>>> assert x.head.tail == Ty()
>>> assert x.delay().head == Ty()
>>> assert x.delay().tail == x

In the category of streams, this is just the identity.