Diagram#

class discopy.pivotal.Diagram(inside, dom, cod, _scan=True)[source]#

Bases: discopy.rigid.Diagram, discopy.traced.Diagram

A pivotal diagram is a rigid diagram and a traced diagram with pivotal types as domain and codomain.

Parameters:

  • inside (Layer) – The layers of the diagram.

  • dom (Ty) – The domain of the diagram, i.e. its input.

  • cod (Ty) – The codomain of the diagram, i.e. its output.

ty_factory#

alias of Ty

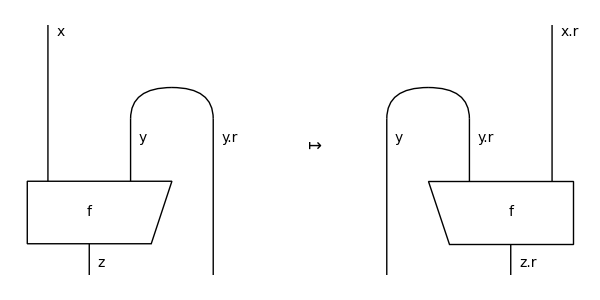
dagger()[source]#

The dagger of a pivotal diagram is its vertical reflection.

Example

>>> x, y, z = map(Ty, "xyz")
>>> f = Box('f', x @ y, z).curry()

>>> from discopy.drawing import Equation
>>> Equation(f, f.dagger(), symbol="$\\mapsto$").draw(
...     figsize=(6, 3), asymmetry=.1,
...     path="docs/_static/pivotal/dagger.png")
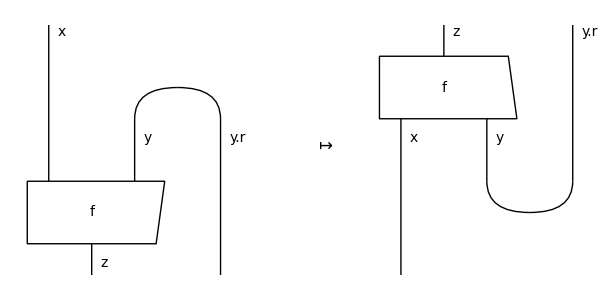
../_images/dagger1.png
conjugate()[source]#

The horizontal reflection of a diagram, defined as the dagger of the rotation.

Equivalently, it is the rotation of the dagger.

Example

>>> x, y, z = map(Ty, "xyz")
>>> x, y, z = map(Ty, "xyz")
>>> f = Box('f', x @ y, z).curry()
>>> assert f.conjugate() == f[::-1].rotate() == f.rotate()[::-1]

>>> from discopy.drawing import Equation
>>> Equation(f, f.conjugate(), symbol="$\\mapsto$").draw(
...     figsize=(6, 3), path="docs/_static/pivotal/conjugate.png")
../_images/conjugate.png
classmethod trace_factory(diagram, left=False)[source]#

The trace of a pivotal diagram is its pre- and post-composition with cups and caps to form a feedback loop.

Parameters:

  • diagram (Diagram) – The diagram to trace.

  • left – Whether to trace on the left or right.

cap_factory#

alias of Cap

cup_factory#

alias of Cup

factory#

alias of Diagram