Hypergraph

class discopy.hypergraph.Hypergraph(dom, cod, boxes, wires, spider_types=None, offsets=None)

Bases: Composable, Whiskerable, NamedGeneric['category', 'functor']

A hypergraph is given by:

• a domain, a codomain and an n-tuple of boxes

• a Wiring triple dom_wires, box_wires, cod_wires where

  • (dom_wires, cod_wires) is the Boundary of the hypergraph

  • box_wires: tuple[Boundary, ...] is the boundary of each box

• an optional mapping SpiderTypes from spiders to types

A Boundary is just a pair of input and output Wires.

Wires are n-tuples of Spider labels.

Spider labels can be of any type.

Parameters:

• dom (category.ob) – The domain of the diagram, i.e. its input.

• cod (category.ob) – The codomain of the diagram, i.e. its output.

• boxes (tuple[category.ar, ...]) – The boxes inside the diagram.

• wires (Wiring) – List of wires from ports to spiders.

• spider_types (SpiderTypes) – Optional mapping from spiders to atomic types, if None then this is computed from the types of ports.

• offsets (tuple[int | None, ...]) – tuple[int | None, …] Number of wires left of each box, used by to_diagram().

Note

Abstractly, a hypergraph diagram can be seen as a cospan for the boundary:

range(len(dom)) -> range(n_spiders) <- range(len(cod))

together with a cospan for each box in boxes:

range(len(box.dom)) -> range(n_spiders) <- range(len(box.cod))

Composition of two hypergraph diagram is given by the pushout of the span:

range(self.n_spiders) <- range(len(self.cod)) -> range(other.n_spiders)

Note

The Hypergraph class is parameterised by a Category, i.e. instances of Hypergraph[C] have dom: C.ob and cod: C.ob as boundary and boxes: tuple[C.ar, ...] as generators. For example:

>>> from discopy.frobenius import Hypergraph as H
>>> from discopy.frobenius import Ty, Diagram
>>> assert H.category.ob == Ty and H.category.ar == Diagram

They are also parameterised by a Functor called by to_diagram().

>>> from discopy.frobenius import Functor
>>> assert H.functor == Functor

Examples

>>> x, y, z = map(Ty, "xyz")

>>> assert H.id(x @ y @ z).n_spiders == 3
>>> assert H.id(x @ y @ z).wires ==((0, 1, 2), (), (0, 1, 2))

>>> assert H.swap(x, y).n_spiders == 2
>>> assert H.swap(x, y).wires == ((0, 1), (), (1, 0))

>>> assert H.spiders(1, 2, x @ y).n_spiders == 2
>>> assert H.spiders(1, 2, x @ y).wires ==((0, 1), (), (0, 1, 0, 1))
>>> assert H.spiders(0, 0, x @ y @ z).n_spiders == 3
>>> assert H.spiders(0, 0, x @ y @ z).wires == ((), (), ())

>>> from discopy.frobenius import Box
>>> f, g = Box('f', x, y).to_hypergraph(), Box('g', y, z).to_hypergraph()

>>> assert f.n_spiders == g.n_spiders == 2
>>> assert f.wires == g.wires == ((0, ), (((0, ), (1, )), ), (1, ))

>>> assert (f >> g).n_spiders == 3
>>> assert (f >> g).wires == ((0,), (((0,), (1,)), ((1,), (2,))), (2,))

>>> assert (f @ g).n_spiders == 4
>>> assert (f @ g).wires == ((0, 1), (((0,), (2,)), ((1,), (3,))), (2, 3))

property spider_wires: list[tuple[set[int], set[int]]]

The input and output wires for each spider of a hypergraph.

Example

>>> from discopy.frobenius import Ty, Box, Hypergraph as H

>>> x, y, z = map(Ty, "xyz")
>>> f = Box('f', x, y).to_hypergraph()
>>> for wires in (f >> H.spiders(1, 2, y)).spider_wires: print(wires)
({0}, {1})
({2}, {3, 4})

property ports

The ports in a diagram.

Examples

>>> from discopy.frobenius import Ty, Box, Hypergraph as H

>>> x, y, z = map(Ty, "xyz")
>>> f = Box('f', x, y @ y).to_hypergraph()
>>> g = Box('g', y @ y, z).to_hypergraph()
>>> for port in (f >> g).ports: print(port)
Node('input', i=0, obj=frobenius.Ty(frobenius.Ob('x')))
Node('dom', depth=0, i=0, obj=frobenius.Ty(frobenius.Ob('x')))
Node('cod', depth=0, i=0, obj=frobenius.Ty(frobenius.Ob('y')))
Node('cod', depth=0, i=1, obj=frobenius.Ty(frobenius.Ob('y')))
Node('dom', depth=1, i=0, obj=frobenius.Ty(frobenius.Ob('y')))
Node('dom', depth=1, i=1, obj=frobenius.Ty(frobenius.Ob('y')))
Node('cod', depth=1, i=0, obj=frobenius.Ty(frobenius.Ob('z')))
Node('output', i=0, obj=frobenius.Ty(frobenius.Ob('z')))

rebracket(flat_wires, boxes=None, dom=None)

Rebracket a flat list of Spider into a proper Wiring.

Parameters:

flat_wires (list[Any]) –

property n_spiders

The number of spiders in a hypergraph diagram.

property scalar_spiders

The zero-legged spiders in a hypergraph diagram.

then(other)

Composition of two hypergraph diagrams, i.e. their pushout().

Parameters:

other (Hypergraph) –

tensor(other)

Tensor of two hypergraph diagrams, i.e. their disjoint union.

Parameters:

other (Hypergraph) –

dagger()

Dagger of a hypergraph diagram, called with [::-1].

Examples

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x, y, z = map(Ty, "xyz")
>>> f = Box('f', x, y).to_hypergraph()
>>> g = Box('g', y, z).to_hypergraph()
>>> assert (f >> g)[::-1] == g[::-1] >> f[::-1]
>>> assert H.spiders(1, 2, x @ y)[::-1] == H.spiders(2, 1, x @ y)

transpose(left=False)

The transpose of a hypergraph diagram.

rotate(left=False)

The half-turn rotation of a hypergraph, called with .l and .r.

explicit_trace(left=False)

The trace of a hypergraph with explicit boxes (trace, cup or cap).

Parameters:

left – Whether to trace on the left or right.

Note

When category.ar.trace_factory is a subclass of category.ar, e.g. for symmetric diagrams, then the result is just one big trace box wrapped up as a hypergraph.

Otherwise, we assume that the trace factory is a class method, e.g. for compact diagrams, in which case we use this method to introduce cup and cap boxes.

trace(n=1, left=False)

The trace of a hypergraph is its pre- and post-composition with cups and caps to form a feedback loop.

Parameters:

• n – The number of wires to trace.

• left – Whether to trace on the left or right.

interchange(i, j)

Interchange boxes at indices i and j.

Parameters:

• i (int) – The index of the first box.

• j (int) – The index of the second box.

Return type:

Hypergraph

Example

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x = Ty('x')
>>> f = Box('f', Ty(), x).to_hypergraph()
>>> g = Box('g', x, Ty()).to_hypergraph()
>>> print((f >> g).interchange(0, 1))
Cap(x, x) >> g @ x >> f @ x >> Cup(x, x)

simplify()

Simplify by applying interchangers eagerly until the length of the diagram is minimal, takes quadratic time.

Example

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x = Ty('x')
>>> f = Box('f', Ty(), x).to_hypergraph()
>>> g = Box('g', x, Ty()).to_hypergraph()
>>> assert (f >> g).interchange(0, 1).simplify() == f >> g

Return type:

Hypergraph

property bijection

Bijection between ports.

:raises ValueError : If the hypergraph is not bijective.:

Examples

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x, y = map(Ty, "xy")
>>> f = Box('f', x, y).to_hypergraph()
>>> for i, port in enumerate(f.ports): print(i, port)
0 Node('input', i=0, obj=frobenius.Ty(frobenius.Ob('x')))
1 Node('dom', depth=0, i=0, obj=frobenius.Ty(frobenius.Ob('x')))
2 Node('cod', depth=0, i=0, obj=frobenius.Ty(frobenius.Ob('y')))
3 Node('output', i=0, obj=frobenius.Ty(frobenius.Ob('y')))
>>> for i, j in enumerate(f.bijection): print(f"{i} -> {j}")
0 -> 1
1 -> 0
2 -> 3
3 -> 2

property is_bijective: bool

Checks bijectivity, i.e. each spider is connected to two or zero ports. In that case, the diagram actually lives in a compact-closed category, i.e. it can be drawn using only swaps, cups and caps.

Examples

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x, y = map(Ty, "xy")
>>> f = Box('f', x, y).to_hypergraph()
>>> assert f.is_bijective and f.transpose().is_bijective
>>> assert H.cups(x, x).is_bijective and H.caps(x, x).is_bijective
>>> assert H.spiders(0, 0, x).is_bijective
>>> assert not H.spiders(1, 2, x).is_bijective

property is_monogamous: bool

Checks monogamy, i.e. each input connects to exactly one output, formally whether self.wires induces a bijection:

len(self.dom) + sum(len(box.dom) for box in boxes)
== self.n_spiders - len(self.scalar_spiders)
== sum(len(box.cod) for box in boxes) + len(self.dom)

In that case, the diagram actually lives in a traced category.

Examples

>>> from discopy.frobenius import Ty, Box, Hypergraph as H

>>> x, y = map(Ty, "xy")
>>> f = Box('f', x, y).to_hypergraph()

>>> assert f.is_monogamous
>>> assert (f >> f[::-1]).is_monogamous

>>> assert H.spiders(0, 0, x).is_monogamous

>>> cycle = H.caps(x, x) >> x @ (f >> f[::-1]) >> H.cups(x, x)
>>> assert cycle.is_monogamous

>>> assert not f.transpose().is_monogamous
>>> assert not H.cups(x, x).is_monogamous
>>> assert not H.spiders(1, 2, x).is_monogamous
>>> assert not H.spiders(2, 3, x).is_monogamous

property is_left_monogamous: bool

Checks left monogamy, i.e. if each non-scalar spider is connected to exactly one output port.

property is_causal: bool

Checks causality, i.e. if each spider is connected to exactly one output port and to zero or more input ports all with higher indices.

If the diagram is causal then it lives in a symmetric monoidal category with a supply of commutative comonoids.

If the diagram is causal and monogamous then it actually lives in a symmetric monoidal category, i.e. it can be drawn using only swaps.

Examples

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x, y = map(Ty, "xy")
>>> f = Box('f', x, y).to_hypergraph()
>>> assert f.is_causal
>>> assert (f >> H.spiders(1, 0, y)).is_causal
>>> assert (H.spiders(1, 2, x) >> f @ f).is_causal

>>> cycle = H.caps(x, x) >> H.cups(x, x)
>>> assert not cycle.is_causal

>>> assert not H.cups(x, x).is_causal

make_bijective()

Introduces spider boxes to make self bijective.

Example

>>> from discopy.frobenius import Ty, Spider, Hypergraph as H

>>> spider = H.spiders(3, 2, Ty('x')).make_bijective()
>>> assert spider.boxes == (Spider(3, 2, Ty('x')), )
>>> assert spider.wires == ((0, 1, 2), (((0, 1, 2), (3, 4)),), (3, 4))

>>> copy = H.spiders(1, 2, Ty('x', 'y')).make_bijective()
>>> assert copy.boxes == (Spider(1, 2, Ty('x')), Spider(1, 2, Ty('y')))

>>> unit = H.spiders(0, 1, Ty('x', 'y')).make_bijective()
>>> assert unit.boxes == (Spider(0, 1, Ty('y')), Spider(0, 1, Ty('x')))

Return type:

Hypergraph

make_monogamous()

Introduce Cup and Cap boxes to make self monogamous.

Example

>>> from discopy.frobenius import Ty, Box, Cup, Cap, Spider
>>> x = Ty('x')
>>> h = Box('f', x, x).transpose().to_hypergraph().make_monogamous()
>>> assert list(zip(h.boxes, h.box_wires)) == [
...     (Cap(x, x),      ((),     (1, 2))),
...     (Box('f', x, x), ((1,),   (3,)  )),
...     (Cup(x, x),      ((0, 3), ()    ))]

Return type:

Hypergraph

make_left_monogamous()

Introduce spider boxes to make self left monogamous.

Example

>>> from discopy.frobenius import Ty, Box, Hypergraph as H, Spider
>>> h = H.spiders(2, 3, Ty('x')).make_left_monogamous()
>>> assert h.boxes == (Spider(2, 1, Ty('x')), )
>>> assert h.wires == ((0, 1), (((0, 1), (2,)),), (2, 2, 2))

Return type:

Hypergraph

make_causal()

Introduce trace boxes to make self causal.

Example

>>> from discopy.frobenius import Ty, Box, Cup, Cap
>>> x = Ty('x')
>>> f = Box('f', x @ x, x @ x).to_hypergraph()
>>> assert f.trace().make_causal().boxes\
...     == (Cap(x, x), f.boxes[0], Cup(x, x))

>>> from discopy.frobenius import Hypergraph as H, Spider
>>> assert H.spiders(2, 1, x).make_causal().boxes\
...     == (Spider(2, 1, x),)

Return type:

Hypergraph

classmethod from_box(box)

Turn a box into a hypergraph with binary spiders for each wire.

Parameters:

box (Box) – The box to turn into a hypergraph.

Return type:

Hypergraph

Example

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x, y, z = map(Ty, "xyz")
>>> for p in Box('f', x, y @ z).to_hypergraph().ports: print(p)
Node('input', i=0, obj=frobenius.Ty(frobenius.Ob('x')))
Node('dom', depth=0, i=0, obj=frobenius.Ty(frobenius.Ob('x')))
Node('cod', depth=0, i=0, obj=frobenius.Ty(frobenius.Ob('y')))
Node('cod', depth=0, i=1, obj=frobenius.Ty(frobenius.Ob('z')))
Node('output', i=0, obj=frobenius.Ty(frobenius.Ob('y')))
Node('output', i=1, obj=frobenius.Ty(frobenius.Ob('z')))

classmethod from_diagram(old)

Turn a Diagram into a Hypergraph.

Parameters:

old (Diagram) – The planar diagram to encode as hypergraph.

Return type:

Hypergraph

Example

>>> from discopy.frobenius import Ty, Hypergraph as H
>>> x, y = map(Ty, "xy")
>>> back_n_forth = lambda d: H.from_diagram(d.to_diagram())
>>> for d in [H.spiders(0, 0, x),
...           H.spiders(2, 3, x),
...           H.spiders(1, 2, x @ y)]:
...     assert back_n_forth(d) == d

to_diagram(make_causal_first=False)

Downgrade to Diagram, called by print.

Parameters:

make_causal_first (bool) – The order in which we downgrade.

Return type:

Diagram

Note

Hypergraphs can be translated to planar diagrams in two different ways:

• either we first make_bijective() (introducing spiders) then make_monogamous() (introducing cups and caps) and finally make_causal() (introducing traces)

• or we first make_left_monogamous() (introducing merges) then make_causal() (introducing traces) and finally make_bijective() (introducing copies).

Examples

>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x = Ty('x')
>>> v = Box('v', Ty(), x @ x).to_hypergraph()
>>> print(v >> H.swap(x, x) >> v[::-1])
v >> Swap(x, x) >> v[::-1]
>>> print(x @ H.swap(x, x) >> v[::-1] @ x)
x @ Swap(x, x) >> v[::-1] @ x

classmethod from_callable(dom, cod)

Turns an arbitrary Python function into a causal hypergraph.

Parameters:

• dom (Ty) – The domain of the hypergraph.

• cod (Ty) – The codomain of the hypergraph.

Return type:

Callable[Callable, Hypergraph]

classmethod from_graph(graph)

The inverse of to_graph().

Parameters:

graph (DiGraph) –

Return type:

Hypergraph

to_graph()

Translate a hypergraph into a labeled graph with nodes for inputs, outputs, boxes, domain, codomain and spiders.

Return type:

DiGraph

depth()

The depth of a causal hypergraph.

Return type:

int

spring_layout(seed=None, k=None)

Computes a layout using a force-directed algorithm.

draw(seed=None, k=0.25, path=None)

Draw a hypegraph using a force-based layout algorithm.

Examples

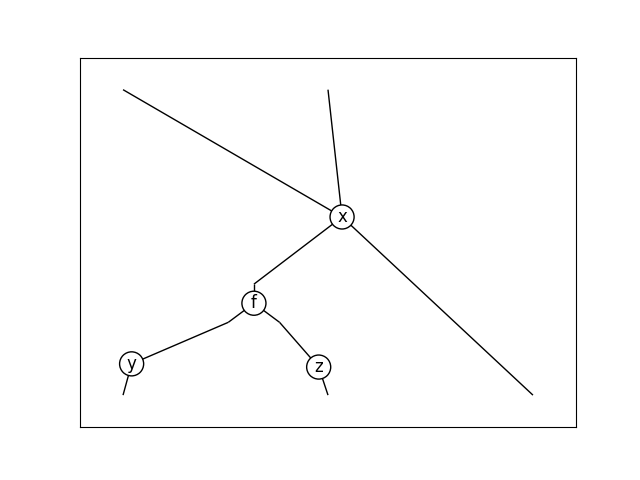
>>> from discopy.frobenius import Ty, Box, Hypergraph as H
>>> x, y, z = map(Ty, "xyz")
>>> f = Box('f', x, y @ z).to_hypergraph()
>>> f.draw(
...     path='docs/_static/hypergraph/box.png', seed=42)

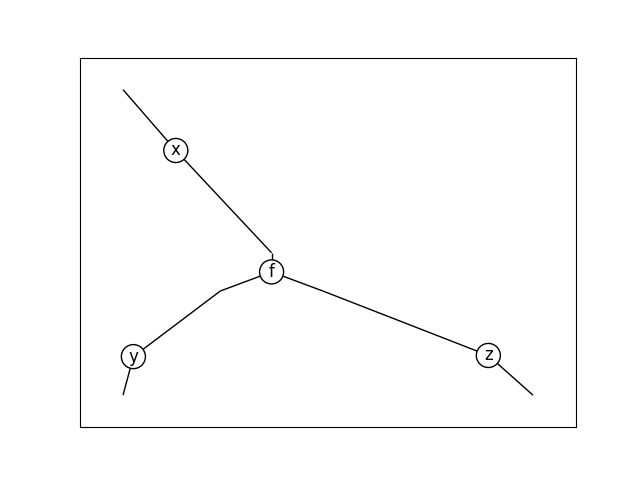
>>> (H.spiders(2, 2, x) >> f @ x).draw(
...     path='docs/_static/hypergraph/diagram.png', seed=42)