Functor

class discopy.rigid.Functor(ob=None, ar=None, dom=None, cod=None)

Bases: discopy.closed.Functor

A rigid functor is a closed functor that preserves cups and caps.

Parameters:

• ob (Mapping[Ty, Ty]) – Map from atomic Ty to cod.ob.

• ar (Mapping[Box, Diagram]) – Map from Box to cod.ar.

• cod (Category) – The codomain of the functor.

• dom (T) –

Example

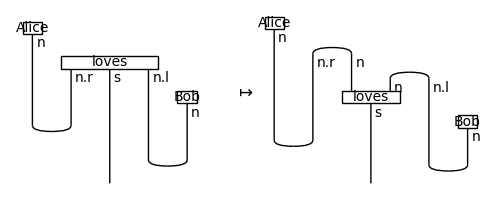
>>> s, n = Ty('s'), Ty('n')
>>> Alice, Bob = Box("Alice", Ty(), n), Box("Bob", Ty(), n)
>>> loves = Box('loves', Ty(), n.r @ s @ n.l)
>>> love_box = Box('loves', n @ n, s)
>>> ob = {s: s, n: n}
>>> ar = {Alice: Alice, Bob: Bob}
>>> ar.update({loves: Cap(n.r, n) @ Cap(n, n.l) >> n.r @ love_box @ n.l})
>>> F = Functor(ob, ar)
>>> sentence = Alice @ loves @ Bob >> Cup(n, n.r) @ s @ Cup(n.l, n)
>>> assert F(sentence).normal_form() == Alice >> Id(n) @ Bob >> love_box

>>> from discopy.drawing import Equation
>>> Equation(sentence, F(sentence), symbol='$\\mapsto$').draw(
...     figsize=(5, 2), path='docs/_static/rigid/functor-example.png')