frobenius

The free symmetric category with a supply of spiders, also known as special commutative Frobenius algebras.

Diagrams in the free hypergraph category are faithfully encoded as Hypergraph, see Bonchi et al. [BGK+22].

Summary

Ob	A frobenius object is a self-dual pivotal object.
Ty	A frobenius type is a pivotal type with frobenius objects inside.
Diagram	A frobenius diagram is a compact diagram and a Markov diagram.
Box	A frobenius box is a compact and Markov box in a frobenius diagram.
Cup	A frobenius cup is a compact cup in a frobenius diagram.
Cap	A frobenius cap is a compact cap in a frobenius diagram.
Swap	A frobenius swap is a compact and Markov swap in a frobenius diagram.
Spider	The spider with n_legs_in and n_legs_out on a given atomic type, with some optional phase as data.
Bubble	A Frobenius bubble is a monoidal bubble in a frobenius diagram.
Category	A hypergraph category is a compact category with a method spiders.
Functor	A hypergraph functor is a compact functor that preserves spiders.

Axioms

>>> from discopy.drawing import Equation
>>> x, y, z = map(Ty, "xyz")

>>> split, merge = Spider(1, 2, x), Spider(2, 1, x)
>>> unit, counit = Spider(0, 1, x), Spider(1, 0, x)

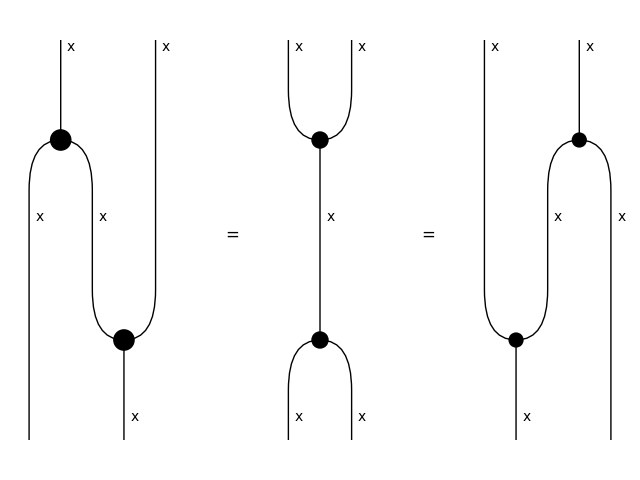
Frobenius

>>> frobenius = Equation(
...     split @ x >> x @ merge, merge >> split, x @ split >> merge @ x)
>>> with Diagram.hypergraph_equality:
...     assert frobenius
>>> frobenius.draw(path="docs/_static/frobenius/frobenius.png")

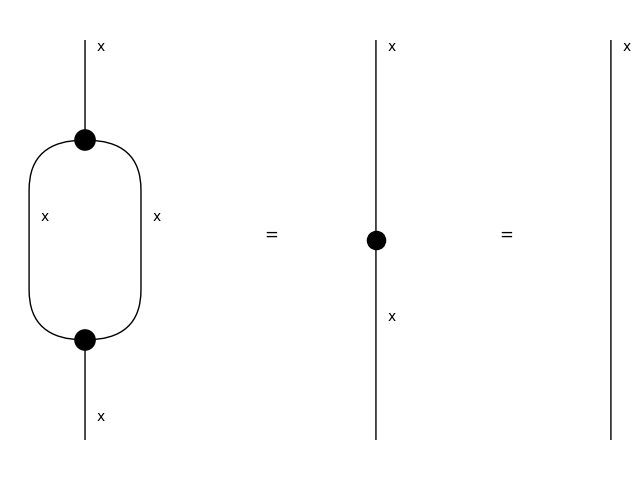
Speciality

>>> special = Equation(split >> merge, Spider(1, 1, x), Id(x))
>>> with Diagram.hypergraph_equality:
...     assert special
>>> special.draw(path="docs/_static/frobenius/special.png")