interaction

The free compact category on a symmetric traced category, or more generally the free ribbon category on a balanced traced category.

Concretely, this is a “glorification of the construction of the integers from the natural numbers”. This so-called Int-construction first appeared in Joyal, Street & Verity [JSV96]. It is sometimes called the “geometry of interaction” construction, see Abramsky [Abr96].

Summary

Ty	An integer type is a pair of natural types.
Diagram	An integer diagram from x to y is a natural diagram from x.positive @ y.negative to x.negative @ y.positive.
NamedGeneric	A NamedGeneric is a Generic where the type parameter has a name.

Functions

Int	The Int construction, returns a ribbon category.

Example

>>> from discopy.grammar import pregroup
>>> from discopy.grammar.pregroup import Word, Cup, Diagram, Functor
>>> s, n = map(pregroup.Ty, "sn")
>>> Alice, loves, Bob\
...     = Word('Alice', n), Word('loves', n.r @ s @ n.l), Word('Bob', n)
>>> who = Word('who', n.r @ n @ (n.r @ s).l)
>>> noun_phrase = Alice @ who @ loves @ Bob\
...     >> Cup(n, n.r) @ n @ Diagram.cups((n.r @ s).l, n.r @ s) @ Cup(n.l, n)

>>> from discopy.frobenius import Ty as T, Diagram as D, Box, Category, Swap
>>> S, N = map(T, "SN")
>>> F = Functor(
...     ob={s: Ty[T](S), n: Ty[T](N)},
...     ar={Alice: Box('A', T(), N),
...         who: Box('W', S @ N, N @ N),
...         loves: Box('L', N @ N, S),
...         Bob: Box('B', T(), N)},
...     cod=Int(Category(T, D)))
>>> image = F(noun_phrase).inside.to_hypergraph().interchange(1, 3)\
...     .to_diagram().interchange(1, 2).naturality(2, left=False)

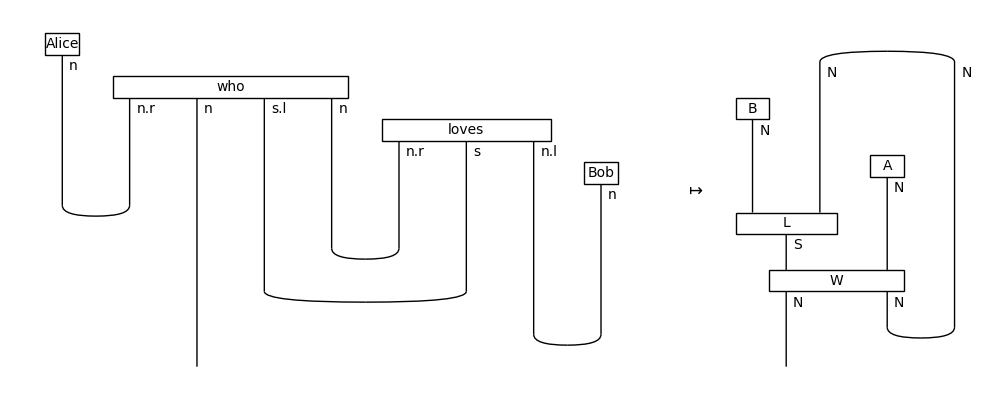
>>> from discopy.drawing import Equation
>>> Equation(noun_phrase, image, symbol="$\\mapsto$").draw(
...     figsize=(10, 4), path="docs/_static/int/alice-loves-bob.png")