symmetric

The free symmetric category, i.e. diagrams with swaps.

Summary

Diagram	A symmetric diagram is a balanced diagram with Swap boxes.
Box	A symmetric box is a balanced box in a symmetric diagram.
Swap	The swap of atomic types left and right.
Sum	A symmetric sum is a balanced sum and a symmetric box.
Category	A symmetric category is a balanced category with a method swap.
Functor	A symmetric functor is a monoidal functor that preserves swaps.

Axioms

>>> from discopy.drawing import Equation
>>> x, y, z, w = map(Ty, "xyzw")
>>> f, g = Box("f", x, y), Box("g", z, w)

Triangle

>>> assert Diagram.swap(Ty(), x) == Id(x) == Diagram.swap(x, Ty())

Hexagon

>>> assert Diagram.swap(x, y @ z) == Swap(x, y) @ z >> y @ Swap(x, z)
>>> assert Diagram.swap(x @ y, z) == x @ Swap(y, z) >> Swap(x, z) @ y
>>> Equation(Diagram.swap(x, y @ z), Diagram.swap(x @ y, z), symbol='').draw(
...     space=2, path='docs/_static/symmetric/hexagons.png', figsize=(5, 2))

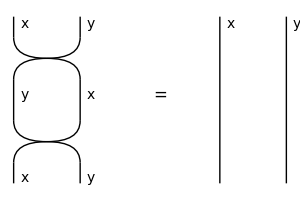
Involution

a.k.a. Reidemeister move 2

>>> assert Swap(x, y)[::-1] == Swap(y, x)
>>> with Diagram.hypergraph_equality:
...     assert Swap(x, y) >> Swap(y, x) == Id(x @ y)
>>> Equation(Swap(x, y) >> Swap(y, x), Id(x @ y)).draw(
...     path='docs/_static/symmetric/inverse.png', figsize=(3, 2))

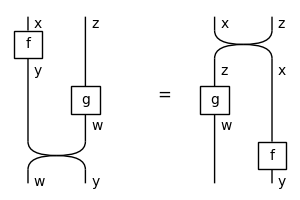
Naturality

>>> naturality = Equation(
...     f @ g >> Swap(f.cod, g.cod), Swap(f.dom, g.dom) >> g @ f)
>>> with Diagram.hypergraph_equality:
...     assert naturality
>>> naturality.draw(
...     path='docs/_static/symmetric/naturality.png', figsize=(3, 2))

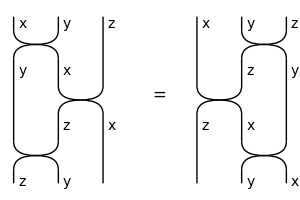
Yang-Baxter

a.k.a. Reidemeister move 3

This is a special case of naturality.

>>> yang_baxter_left = Swap(x, y) @ z >> y @ Swap(x, z) >> Swap(y, z) @ x
>>> yang_baxter_right = x @ Swap(y, z) >> Swap(x, z) @ y >> z @ Swap(x, y)
>>> with Diagram.hypergraph_equality:
...     assert yang_baxter_left == yang_baxter_right
>>> Equation(yang_baxter_left, yang_baxter_right).draw(
...     path='docs/_static/symmetric/yang-baxter.png', figsize=(3, 2))