traced

The free traced category, i.e. diagrams where outputs can feedback into inputs.

Note that these diagrams are planar traced so that e.g. pivotal diagrams are traced in this sense. See symmetric for the usual notion of trace.

Whenever the diagrams are also symmetric, their equality can be checked by translation to monogamous hypergraph.

Summary

Diagram	A traced diagram is a monoidal diagram with Trace boxes.
Box	A traced box is a monoidal box in a traced diagram.
Trace	A trace is a diagram arg with an output wire fed back into an input.
Category	A traced category is a monoidal category with a method trace.
Functor	A traced functor is a monoidal functor that preserves traces.

Axioms

>>> from discopy.drawing import Equation
>>> from discopy.symmetric import Ty, Box, Swap, Id
>>> from discopy import symmetric
>>> symmetric.Diagram.use_hypergraph_equality = True
>>> x = Ty('x')
>>> f, g = Box('f', x @ x, x @ x), Box('g', x, x)

Vanishing

>>> assert f.trace(n=0) == f == f.trace(n=0, left=True)
>>> assert f.trace(n=2) == f.trace().trace()
>>> assert f.trace(n=2, left=True) == f.trace(left=True).trace(left=True)

Superposing

>>> assert (x @ f).trace() == x @ f.trace()
>>> assert (f @ x).trace(left=True) == f.trace(left=True) @ x

Yanking

>>> yanking = Equation(
...     Swap(x, x).trace(left=True), Id(x), Swap(x, x).trace())
>>> yanking.draw(
...     path='docs/_static/traced/yanking.png', draw_type_labels=False)

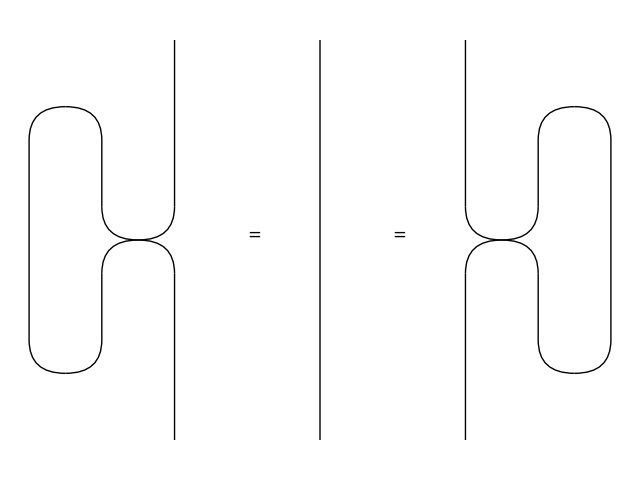
>>> assert yanking

Naturality

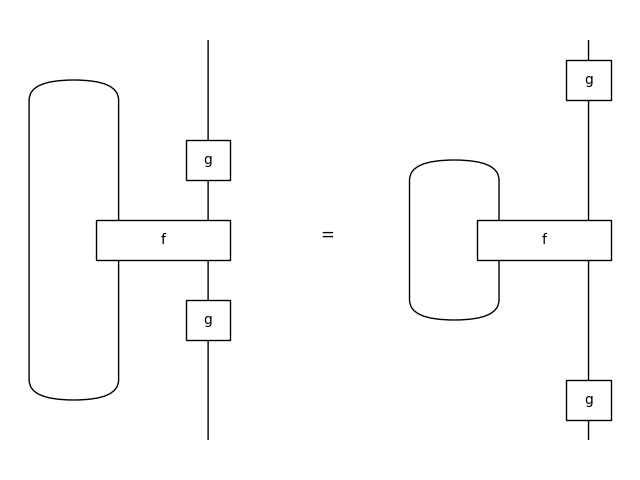
>>> tightening_left = Equation(
...     (x @ g >> f >> x @ g).trace(left=True),
...     g >> f.trace(left=True) >> g)
>>> tightening_left.draw(
...     path='docs/_static/traced/tightening-left.png', draw_type_labels=False)

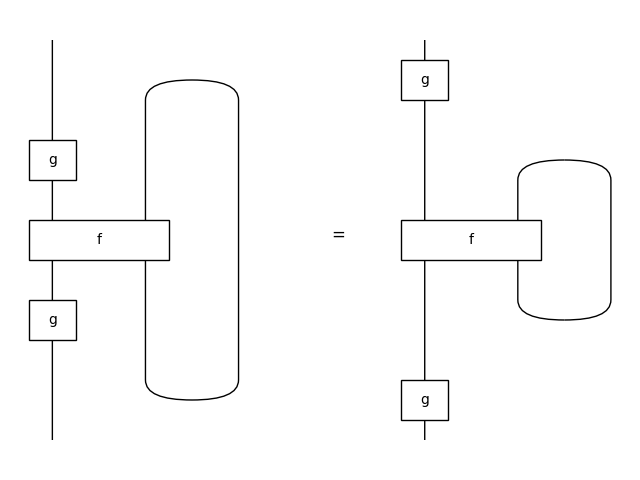
>>> tightening_right = Equation(
...     (g @ x >> f >> g @ x).trace(),
...     g >> f.trace() >> g)
>>> tightening_right.draw(
...     path='docs/_static/traced/tightening-right.png',
...     draw_type_labels=False)

>>> assert tightening_left and tightening_right

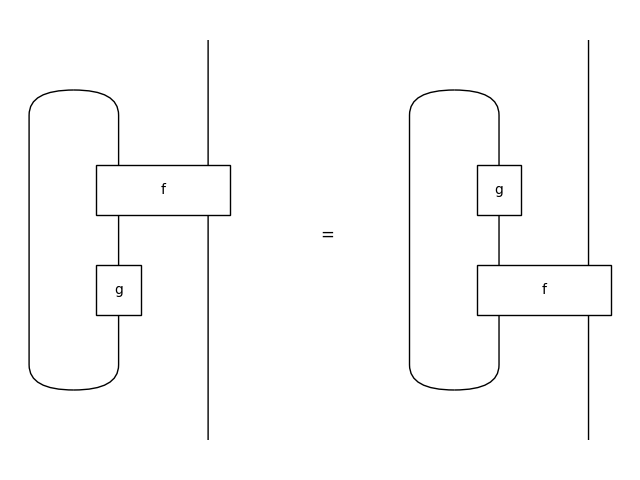
Dinaturality

>>> sliding_left = Equation(
...     (f >> g @ x).trace(left=True),
...     (g @ x >> f).trace(left=True))
>>> sliding_left.draw(
...     path='docs/_static/traced/sliding-left.png', draw_type_labels=False)

>>> sliding_right = Equation(
...     (f >> x @ g).trace(),
...     (x @ g >> f).trace())
>>> sliding_right.draw(
...     path='docs/_static/traced/sliding-right.png', draw_type_labels=False)

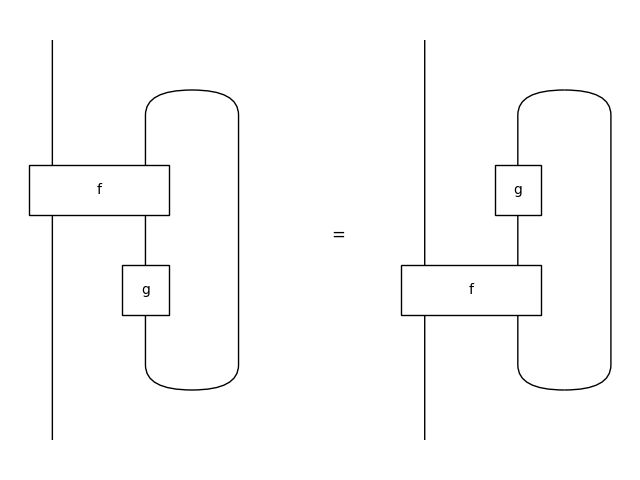
>>> assert sliding_left and sliding_right

>>> symmetric.Diagram.use_hypergraph_equality = False